그래프
- 연결 관계를 표현하는 자료구조
- 정점이라 불리는 데이터를 간선, 혹은 링크로 연결한 형태
- 트리도 사실 그래프의 일종이다.
- 그런데, 트리는 노드간 상하관계를 가지며 사이클 형성 X
- 그래프는 상하관계 X, 사이클 형성 가능 -> 기본적으로 연결 관계를 표현함
| 연결 그래프 | 그래프상의 임의의 두 정점 사이의 경로가 존재하는 그래프 |
| 비연결 그래프 | 어떤 정점 사이에는 경로가 존재하지 않을 수도 있다. |
| 방향 그래프 | 간선에 방향 존재 |
| 무방향 그래프 | 방향이 없는 그래프 |
| 가중치 그래프 | 간선에 가중치가 부여된 그래프. 이 가중치는 비용이라고도 함. |
| 서브그래프(부분 그래프) | 특정 그래프의 정점, 간선의 일부분으로 이루어진 그래프 |
❓이 그래프들은 어떻게 구현하고 저장할까? 노드간 상하관계도 없는데...
인접 행렬 기반 그래프 표현
- N × N 크기의 행렬로 그래프를 표현하는 방법
- N = 정점의 개수
- <행, 열> = <출발 정점, 도착 정점>
- 연결됐을 때는 1, 연결되지 아니하면 0 표기
인접 리스트 기반 그래프 표현
- 그래프의 특정 정점과 연결된 정점들을 연결 리스트로 표현하는 방법
- 각각의 정점마다 연결 리스트를 가지는데, 특정 정점에서 나가는 간선에 연결된 정점들을 연결 리스트의 노드로 삼는다는 의미.
- 가중치 그래프도 인접 리스트로 표현 가능. 하나의 노드를 표현하는 정보에 가중치도 포함하면 됨.
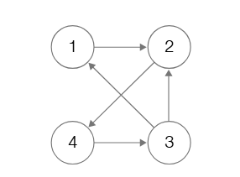

깊이 우선 탐색과 너비 우선 탐색
깊이 우선 탐색 (DFS)
- 그래프에서 더 이상 방문 가능한 정점이 없을 때까지, 최대한 깊이 탐색하기를 반복
- DFS 알고리즘 구현시에는 배열, 스택이 유용.
- 배열: 특정 정점의 방문 여부 확인
- 스택: 뒤로가기 필요시
너비 우선 탐색 (BFS)
- 최대한 넓게 탐색하기를 반복
- 여기서는 배열, 큐가 유용.
- 배열: 방문 여부 확인
- 큐: 연결된 정점들을 저장하기 위해 사용. 즉, 특정 정점과 인접한 모든 정점을 줄 세우듯 저장하고, 앞으로 어떤 정점에서 너비 우선 탐색을 할지 알기 위해...
최단 경로 알고리즘
- 한 정점 -> 목적지 정점까지의 가중치의 합이 최소가 되는 경로 결정
- 대표적으로 다익스트라 알고리즘(Dijkstra's algoritm)
다익스트라 알고리즘
(간선 가중치가 음이 아닌 수라는 가정 하에 사용)
특정 정점 -> 다른 모든 정점까지의 최단 거리 구해 주는 알고리즘
1. 최단 거리 테이블에서 시작 정점을 제외한 정점들: 충분히 큰 수로 초기화
2. (시작)정점 방문
3. 방문 정점과 인접한 정점들 탐색
4. 경로상 가중치 합과, 최단 거리 테이블상의 값 비교
5. 최단 거리 테이블을 갱신할 수 있다면 갱신
6. 방문하지 않은 정점 중 최단 거리가 가장 작은 정점 방문
7. 더 방문할 정점이 없을 때까지 3~6 반복 후 종료